Convergence Analysis for Robust Mode

This document provides an overview of the validation performed for the Robust Convergence Mode in HERA.

Overview

The purpose of this analysis was to ensure that the default parameters used in the robust convergence mode are effective across a variety of data scenarios. Rather than a formal theoretical study, this was a practical validation using Monte Carlo simulations to verify that convergence is reliably achieved within the default iteration limits across typical use cases.

Additionally, we evaluated the accuracy of the results by comparing them against reference values generated with a very high number of bootstrap iterations. This ensures that the convergence criteria not only stop at a reasonable time but also produce results with acceptable error relative to the reference values.

The results confirm that the default settings are appropriate for the vast majority of scenarios, yielding both stable and accurate outcomes.

To ensure reproducibility and fair comparability between the Robust Mode and the reference runs, we utilized a fixed random seed for all simulations. This guarantees that both the convergence checks and the reference benchmarks were performed on identical data sequences and bootstrap samples.

Analysis Design & Constraints

To validate the robustness of the default parameters, we simulated a diverse set of conditions.

Fixed Parameters

It is important to note that the following parameters were treated as constants and thus their influence was not explicitly tested in this analysis:

• Step Size (\(B_{step}\))
• Tolerance (\(Tol\))
• Start Iterations (\(B_{start}\))
• End Iterations (\(B_{end}\))

These were held constant because the three parameters we did test (regarding data distribution and method variability) were considered the most critical factors influencing the stability of achieving a desired tolerance.

Evaluated Scenarios

We tested against multiple distribution types (Normal, Bimodal, Skewed, Likert) and sample sizes, as well as varying method properties.

Data Scenarios:

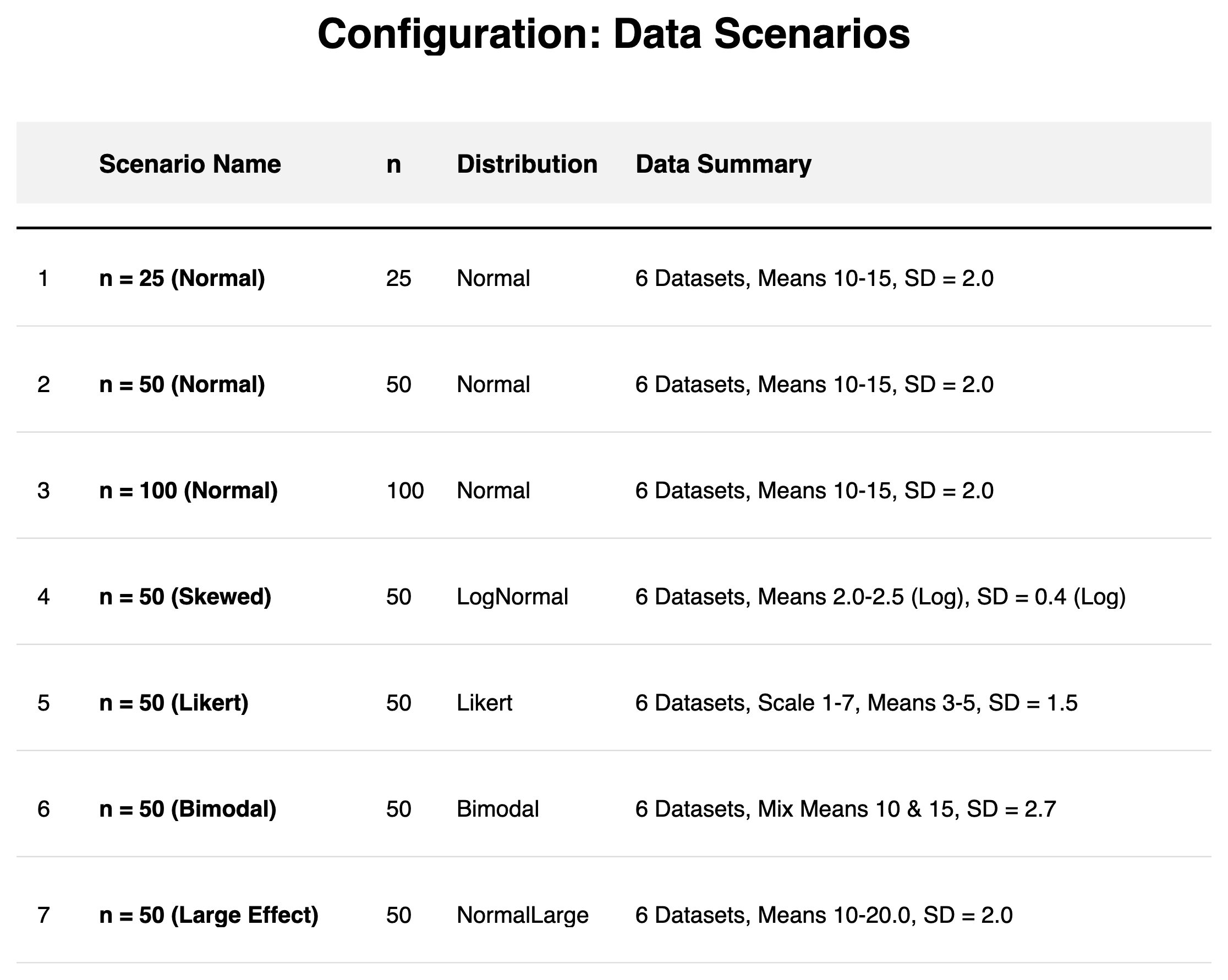
Method Configurations:

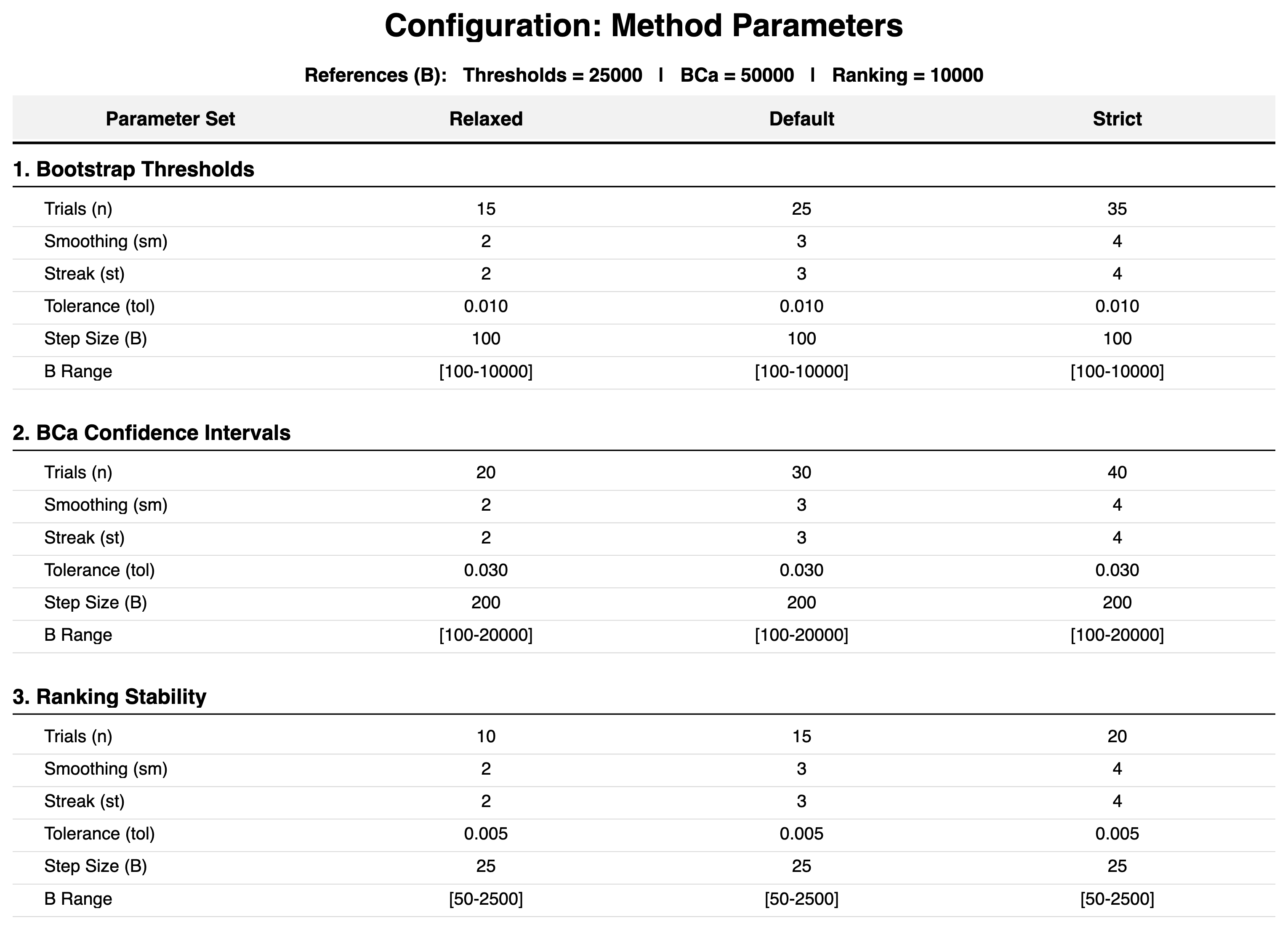
Analysis Scope

To isolate the behavior of individual convergence algorithms, the following simplifications were applied:

• Effect Size Metrics: Both Cliff's Delta and Relative Difference are always calculated, and the convergence criterion is based on the averaged stability of both. Only Cliff's Delta was used as the accuracy metric for comparison against reference values. This design choice allows us to test whether the averaged convergence approach produces accurate individual estimates despite relying on a combined stability indicator.
• Ranking Stability: A single-metric ranking (M1 only) was used to provide a stable reference point. Multi-metric rankings (M1_M2, M1_M2_M3) may exhibit different convergence characteristics due to increased complexity.
• Thresholds for Ranking: Pre-calculated reference thresholds were used to isolate the ranking convergence behavior from threshold estimation variability.

Validation Results

We evaluated the performance of the Robust Mode based on two key criteria: Convergence Success (did it finish?) and Accuracy (were the results correct?).

1. Convergence Frequency

In our analysis, we observed that:

• The Robust Mode achieved exceptionally high convergence rates.
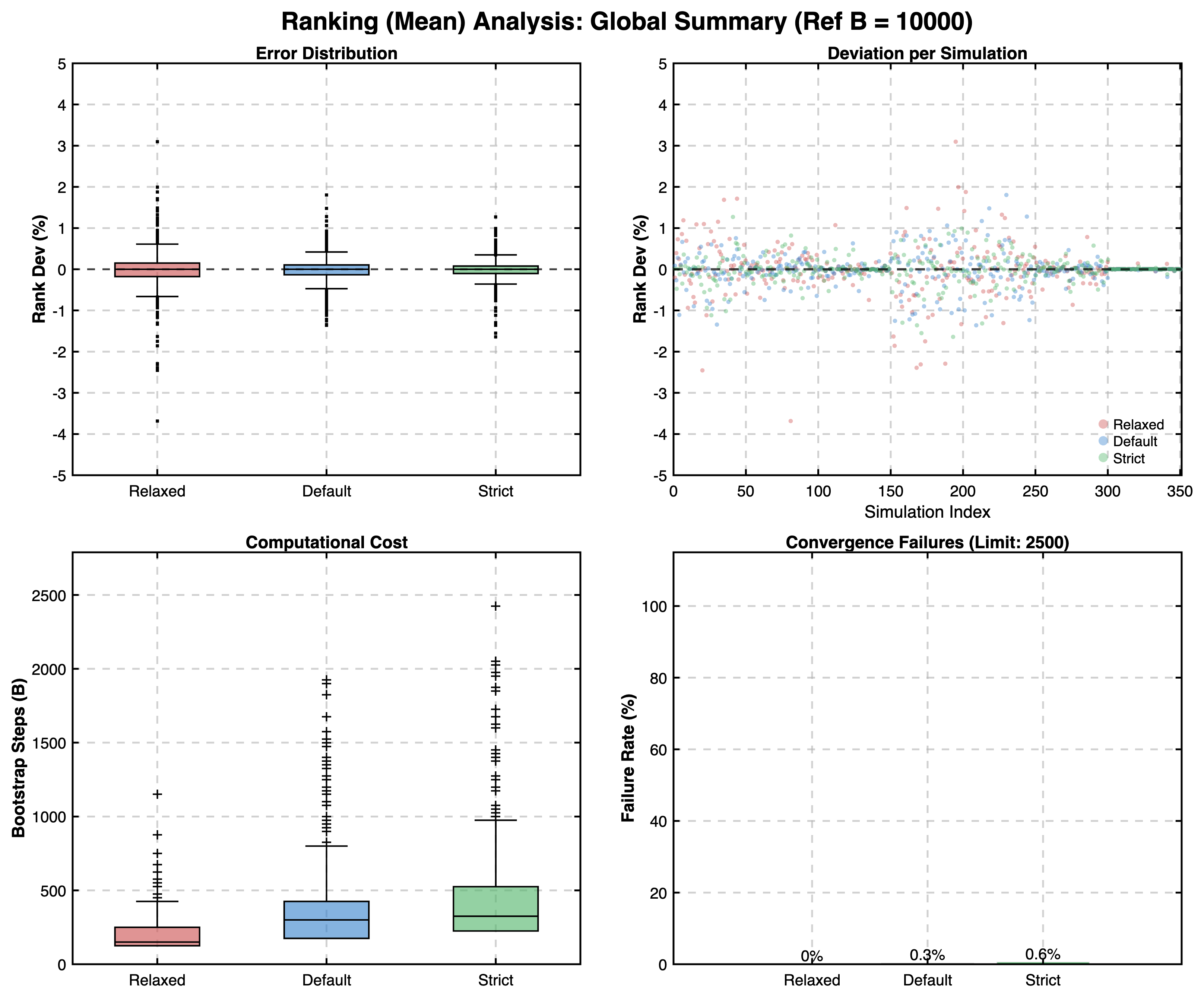
• The Ranking phase was the only area where non-convergence was observed, and even then, it occurred in < 0.3% of ranking cases.
• This implies that for all other metrics (BCa Intervals, Thresholds), convergence was virtually 100%.
• In the rare ranking failures, the maximum number of iterations (B_end) was reached before the convergence criterion was satisfied. To resolve this we increased B_end for the default settings provided.

2. Accuracy Validation

Beyond simply checking for convergence, we also validated the accuracy of the results.

• We compared the outcomes of the Robust Mode against "Gold Standard" reference values generated with very high bootstrap iteration counts:
• Thresholds: \(B_{ref} = 15{,}000\)
• BCa Confidence Intervals: \(B_{ref} = 30{,}000\)
• Ranking Stability: \(B_{ref} = 5{,}000\)
• The goal was to analyze the distribution of errors (deviation from reference) to ensure that the convergence method yields results that are not just stable, but also practically in line with the theoretical limits.
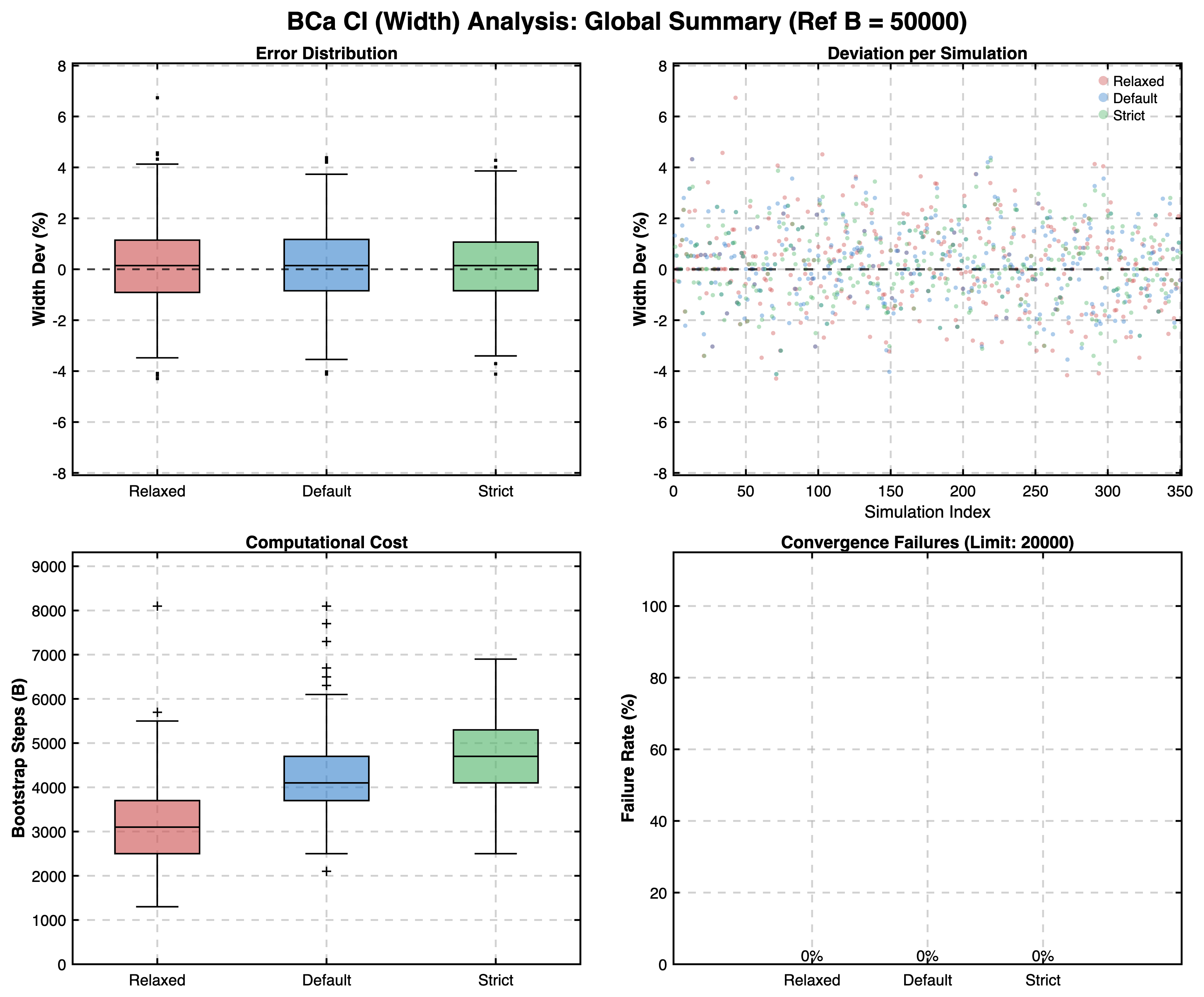
• The results confirmed that the Robust Mode produces estimates with acceptably small deviation from reference values across all simulated scenarios. Median absolute errors were typically well below 5% relative to the reference values. This also validates the averaged convergence approach: despite determining convergence from a combined stability indicator, the individual accuracy of Cliff's Delta remained excellent.

Global Results Summary

Ranking Convergence:

BCa Confidence Interval Convergence:

Threshold Calculations:

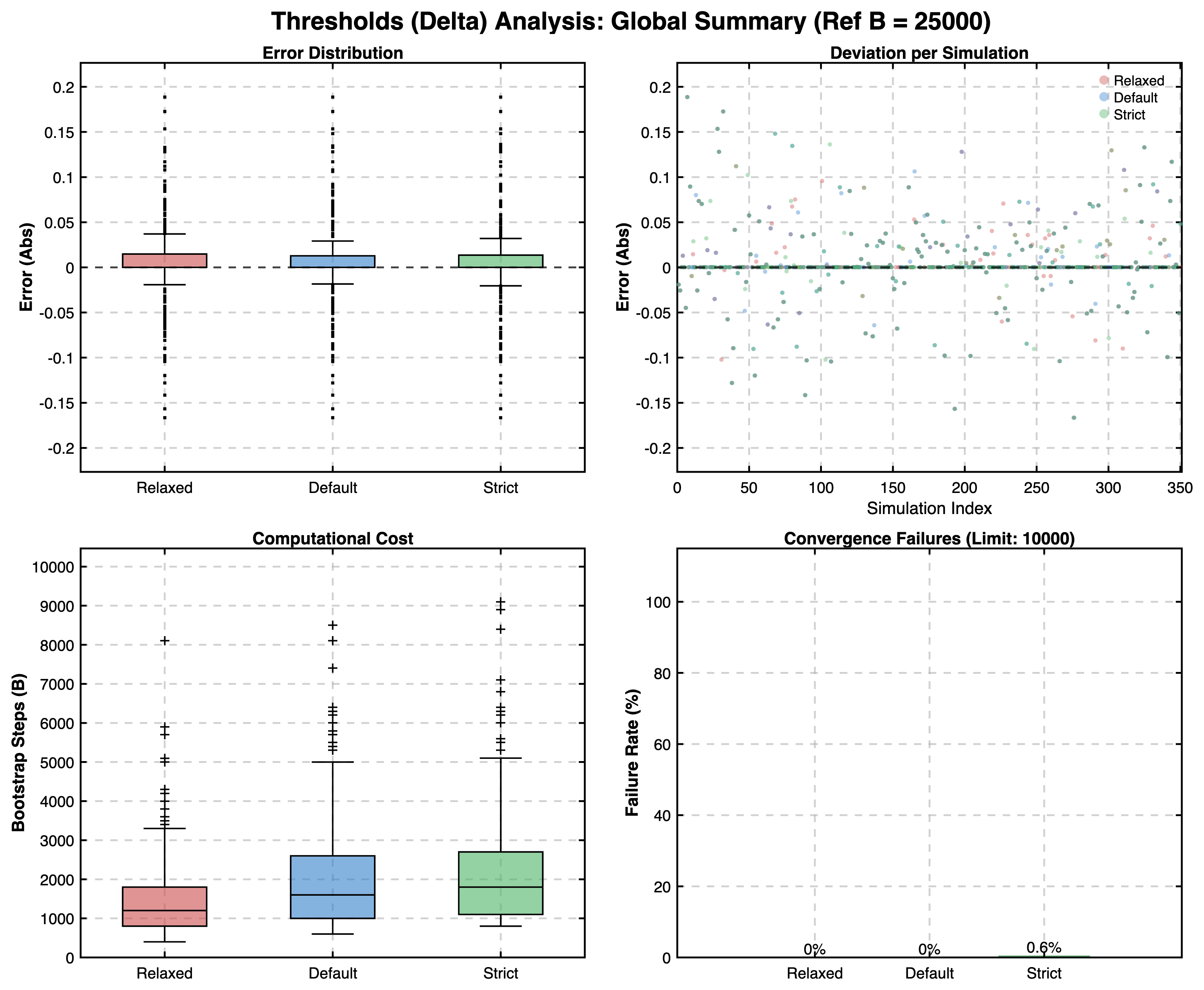
Discussion: Convergence Modes

Based on these results, we can discuss the theoretical implications of the different convergence parameters one could set in HERA compared to the default settings:

• Relaxed: Prioritizes speed. While significantly faster, it carries a higher risk of terminating before true stability is reached, especially in complex scenarios and BCa confidence intervals.
• Strict: Prioritizes guaranteed stability. It enforces rigorous checks that may lead to very high iteration counts. While safer, this can be computationally expensive and potentially overkill for well-behaved datasets where the Default mode would suffice. Also it could lead to non-convergence in some cases for the desired tolerance.
• Default: Designed to balance efficiency and reliability, it seems to be the best option for general usage. Interestingly, in some tested scenarios it provides higher accuracy for the BCa confidence intervals compared to stricter settings when comparing to the reference values. This is likely because stricter settings with more iterations can occasionally include rare extreme bootstrap samples that increase variance without improving the central estimate.

Conclusion

Our analysis confirms that the Default settings provided with HERA should be a safe choice for general usage, achieving convergence in >99.7% of tested Ranking cases and virtually 100% of other cases, while maintaining high accuracy against reference standards.

Computational Note

The complete analysis (7 scenarios × 50 independent simulations, comprising 2,100 distinct datasets) was performed on a standard consumer laptop (Base Model Apple 16" 2021 M1 MBP, 16 GB RAM) in approximately 15 hours. For each simulation, high-precision reference values were independently derived (up to B=30,000 for BCa), followed by convergence tests for all three modes (Relaxed, Default, Strict) utilizing 10–40 stability trials per B-step. This demonstrates the computational efficiency of the parallelized MATLAB implementation.

Full Report

For a comprehensive look at the data, including specific breakdowns for each distribution type, please refer to the generated PDF report:

Download Full Combined Report (PDF)